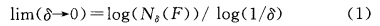吴贤振 ,喻圆圆,刘建伟 ,胡龙飞 ,尹丽冰
(江西理工大学 江西省稀土资源高效利用重点实验室,江西赣州 341000)
摘要 :应用分形理论的盒维数方法,建立双尺度矩形盒维数模型 ,对井下N-FL爆破地表振动实测信号进行分析。介绍了爆破振动信号盒维数D和拟合参数b的计算方法,并获得所测各点的T(切向)、V(垂向)、L(径向)三个方向的爆破振动信号的盒维数D和拟合参数 b;结合爆破振动信号的频谱图,对不同方向爆破振动信号的分形特征进行了探讨。初步研究表明:不同方向的爆破振动信号都表现出盒维数D值越大 ,信号高频成分越多,反之则越少的特征 ;爆破药量对拟合参数b值大小的影响呈类似规律。
关键词 :爆破振动信号;分形理论;盒维数;不同方向;频谱中图分类号 :TD235文献标识码:Adoi:103969/i.issn1006—70512014.04.002
FRACTAL CH ARACTERISTICS OF DIFFERENT
DIRECTIONAL BLASTING VIBRATION SIGNALS
WU Xian—zhen,yUYuan—yuan,LIUJian—wei,HULong—fei,YIN Li—bing
(JiangxiKeyLaboratoryofHighEfficientUtilizationofRareEarthResources,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)
ABSTRACT:U singthebox dimension methodoffracta1theory,thedouble-scaled rectanglebox dimensionmodewasbuilt. Throughanalyzing thesurfacevibration ofdeep hole blasting in the shafts,and introdu—cing thecalculation methodaboutbox dimension and fittingb-valuesofblasting vibration signals,theboxdim ension and fitting6一valuesaboutT ,V ,L ofblasting vibration signalsinthreedirectionshovebeen ob—tained.Com bining with the blasting seismic wave spectrum , fractalcharacteristics ofblasting vibrationsignalsindirectionswerediscussed.Theresultshaveshown thatthegreaterbox dim ension are,them orethehighfrequencycomponentsofsignalhaveandtheblasting quantityhasthesim ilarinfluenceonb-valuesofblasting vibration in variousdirections.
KEY W ORDS:Blasting vibration signals;Fraetaltheory;Box dim ension;Differentdirections;Spectrum
1 引 言
爆破地震波是爆炸应力波在岩体介质中经过多次叠加或衰减产生,携带能量较少,但会对振动区周围的构筑物等产生不良影响。
爆破振动信号可以反映爆区结构特征,爆破振动信号的频率特征与爆破参数、传播介质有着紧密联系。分形盒维数可以很好地描述爆破振动信号,在分形分析中,分形盒维数已运用于诸多领域,是应用最广泛的分形维数之一。龙源等根据爆破地震波的分形盒维数,探讨了爆破地震波分形的物理力学机制,提出了盒维数能够反映岩石(体)介质的特征信息,并从多个角度
对爆破振动信号的分形特征进行了研究H ”。朱权洁等应用小波分形特征,以指定特征频带上重构信号的分形盒维数为信吴贤振等:不同方向爆破振动信号的分形特征号特征,对矿山微震波形进行了识别研究。多数爆破振动信号的分形特征研究 是基于单向或复合信号展开的,而针对不同方向的爆破振动信号分形特征还有待研究。结合分形盒维数,对不同方向爆破振动信号的分形特征进行分析研究,有利于进一步揭示爆破地震波的传播机制,进而有效预防和控制爆破振动灾害。
2 井下深孔爆破地表振动 实测
2.1爆破实施概况
某铀矿井下深孔爆破的爆区试验采场沿阶段高度自下而上划分为126、146m 两个分层 。第一次爆破126m分层,爆破装药量6528kg,炮孔195个,共16段,其中最大一段起爆药量607.5kg;第二次爆破146m分层,爆破装药量9408kg,炮孔292个,共16段,其中最大一段起爆药量为722.25kg。根据爆区地表条件和测试要求,两次测试均布置在地面的同一测点上,4个测点近似一条直线 。
2.2 爆破 测试
两次爆破地表振动效应实测采用的是产自加拿大的BlastmateIll型测振仪。该仪器结构坚固,用微电脑控制进行测速,可同时测试T(切向)、V(垂向 )、L(径向 )三个方向的爆破振动信号,采样频率设置为1024Hz。表1为两次爆破振动测试结果。
表1井下深孔爆破地表振动测试数据。
Table1 Testing dataofsurfacevibration with deepholeblastingintheshafts
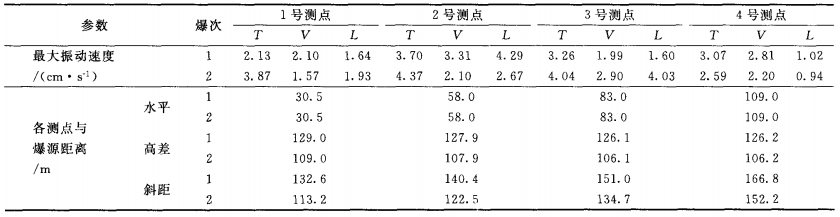
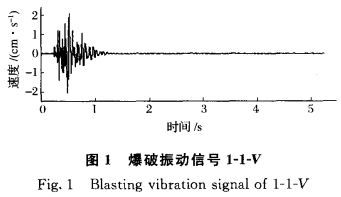
爆破振动信号分形特征在MATLAB7.0软件平台下,以爆破振动信号1—1一VtN点1第一次爆破所测的方向的爆破振动信号)为例进行讨论。图1为爆破振动原始信号,其最大幅值一2.10cm/s。设△£为采样时间(At一1/1024s),T2为有效持续时间,T为主振周期。
3.1分形盒维数概念
分形盒维数是分形理论的基本维数之一 ,已经在科学测量中广泛应用,只需要简单地对盒子计数,保存统计数据后计算即可 ,很容易在计算机中实现,不仅能够适用于自相似的形状 ,也能够适用于非自相似的形状,甚至适用于高维空间中的对象。
设R为维欧式空问,F是其任意非空有界子集,对于任意8> 0,N(F)为直径不大于时,可覆盖F集的最少个数,如果极限
存在,则称该极限值为F的盒维数,记为D。
由式(1)可知,对F集进行覆盖的最少闭球个数服从幂定律,即

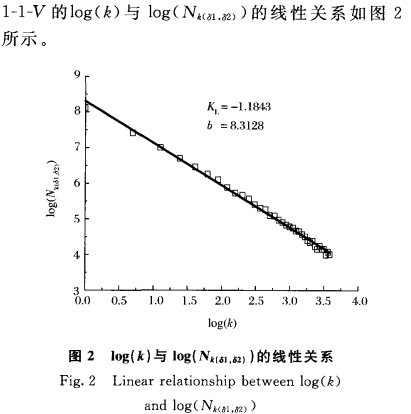
的渐进线近似一条直线,其斜率的相反数就是盒维数D,截距为拟合参数b。
3.2 爆破振动信号盒维数计算
3.2.1 确定有效持续时间与主振周期
由于所测爆破振动信号不全是有用数据,文中只对爆破振动的有效振动持续时间内的数据进行分析。假设各次记录振动强度的最大峰值为Amax,则有效振动持续时间为振动强度初次达到Amax /20至最后衰减为Amax/20这一过程所经历的时间。信号 1—1一V中,Amax/20= 2.10/20=0.105cm/s,第一次达到0.105cm/s和最后衰减到0.105cm/s分别为第252个数据点一0.114cm/s和1095个数据点一 0.114cm/s,所以Tz=(1095—252)At一843At。
文中近似地把爆破地震波波形曲线的最高(或最低)峰值所对应的波峰(或波谷)与横坐标的两交点间距离 的两倍作为主振周期。信号1—1一只有一个最大振幅,即一2.10cm/s,处于第534个数据点,由最高峰值所处的半周期曲线与横坐标两交点间的距离为35.55个采样间隔,近似为36,则主振周期为T=2× 36At===72At。若爆破地震波的最大波峰(或波谷)多于一个,则取所有最大波峰(或波谷)与横坐标交点间的最小距离为半个主振周期。
3.2.2 确定矩 形盒 尺度
爆破地震波形不同于Cantor集 、Koch曲线或Sierpinski地毯等标准分形几何图形,时间和幅值是它的横向尺度和纵向尺度,具有双尺度性。如果用边长为是的正方形格子来覆盖爆破地震波,如同用时间(或幅值)的单位工具来同时测量时间和幅值,则无法同时反映它们的无标度性,故采用双尺度矩形格子对爆破地震波曲线进行覆盖 。
爆破振动信号是具有复杂性和随机性的离散型采样信号,在矩形盒的覆盖下,矩形盒的双尺度不应该覆 盖爆破地震波曲线的周期性和振幅特性,只有同时考虑爆破地震波的周期性和振幅特性,才能有效地确定矩形盒双尺度参数。爆破振动波形图是一系列的离散点连接而成,而相邻数据点之间的横向距离为采样时问间隔△t。当小于At(此时忌< 1)时是没有考虑价值的,所以k的取值必须大于或等于1。与爆破地 震波曲线相交的矩形网格在坐标平面内还要能够表现信号的振幅特征和周期性,可以确定k的最高取值为k<[T/(2At)+1],所测信号的最大k值如表2所示 。
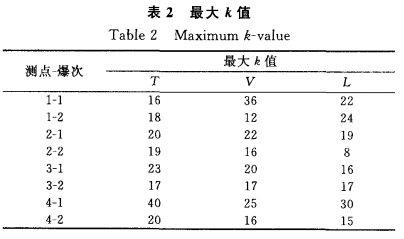
综合各方面因素的考虑和分析,可以将矩形网格的横向尺度确定为=△t;纵向尺度确定为=△Amin(△Amin是爆破振动曲线中相邻点间最小非零幅值差);k的取值范围定为1≤k< [T/(2△t)+ 1],即1≤k<37(其中k为整数)。
3.2.3 计算分形盒维数及线性拟合
将爆破振动信号1-1一V有效振动持续时间Tz内的数据设为离散序列:s(n*△t),n=1,...,N。其中,△t 为采样间隔时间;N一=844,为爆破振动有效持续时间内的采样点个数 。
3.3 计算结果分析
根据以上爆破振动信号分形盒维数计算方法,对所有振动信号T、V、L三个分维 向量的波形曲线的盒维数进行计算,得到爆破振动信号的盒维数D值及拟合参数 b值,如表3所示。图3为不同方向最大、最小盒维数值对应的爆破振动信号的波形图、频谱图 。
表3爆破振动信号的盒维数值及b值
Table3 Theboxdimension and b-value ofblasting vibrationsignal
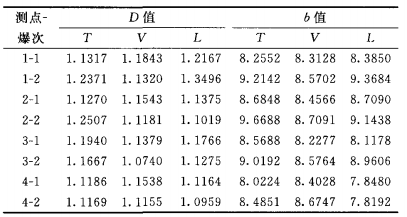
结合表3与图3,对不同方向爆破振动信号分形特征进行分析:(1)对于所有爆次而言,相同测点及相同方向信号的分形盒维数D比较稳定;对比同一测点和同一爆次下爆破振动信号T、V、L三个方向的分形盒维数,发现同一爆源、同一场地 介质条件下,T、V、L三个方向的爆破振动信号的复杂程度有一定的差别,分形盒维数可以反映岩体内部质点振动规律。第二次爆破T、V、L三个方向的b值绝大部分比第一次爆破的大,说明爆破药量是影响b值的主要因素 一 。
(2)爆破振动信号波形曲线的复杂程度可以根据它的频率成分体现出来,对比分 析T、V、L 三个方向最大、最小盒维数D值分别对应的信号波形图与频谱图可知 ,不同方向爆破振动信号 的盒维数值与频率成分之间的关系表现出较好的一致性:盒维数D值越大,波形的起伏就越大,曲线中相邻两点间的相关性就越小 ,信号的高频成分相对较多;反之,信号的盒维数D值越小,波形的波动越小,曲线中相邻两点间的相关性则越大,信号的高频成分就相对较少 。
4 结论
(1)初步研究表明,分形盒维数在爆破振动信号的T(切向)、(垂向)、L(径向)三 个方向上都表现了类似的规律,能够很好地表征爆破振动信号:高频成分所占比例较高时爆破振动信号分形盒维数相对较高,而高频成分所占比例较低时其分形盒维数也相对较低 。
(2)爆破药量是影响不同方向爆破振动信号的拟合参数b值的主要因素之一,爆破总药量和最大段药量越大,在不同方向爆破振动信号的拟合参数b值都呈现出越大的特点,反之则越小 。
参考文献 :
[1]李夕兵 ,凌同华 ,张义平,爆破震动信号分析理论与技【M】.北京 :科学出版社,2009:17—25.
[2]尚晓江,丁桦,爆破近区地质结构特性对震动信号传播的影响研究[J].程爆破,2005,11(3):57—61.
[3]张济忠.分形[M].北京:清华大学出版社,1995:122—127.
[4]晏俊伟,龙源,娄建武等.爆破地震波的分形机制[J].解放军理工大学学报(自然科学版),2008,9(4):367—37Z.
[5]龙源,晏俊伟,娄建武等.基于分形理论的爆破地震信号盒维数研究[J].科技导报,2007,25(18):27—31.
[6]娄建武,龙源,徐全军等.爆破地震信号分形维数计算的矩形盒模型[J].振动与冲击,2005,24(1):81—84.
[7]晏俊伟,龙源,唐献述等.基于分形盒维数的爆破震动信号研究[J].矿冶工程,2007,27(1):13—16.
[8]钟明寿,龙源,谢全民等.基于分形盒维数和多重分形的爆破地震波信号 分析[J].振动与冲击,2010,29(1):711.
[9]谢全民,龙源,田作威等.爆破振动信号时频特征的三维分形特性研究[J].振动与冲击,2010,29(12):118—121.
[10]谢全民,龙源,钟明寿等.小波包与分形组合技术在爆破振动信号分中的应用研究[J].振动与冲击,2011,30(1):11-15.
[11]谢全民,龙源,钟明寿等.小波与分形组合分析技术在爆破振动信号分析中的应用[J].振动与冲击,2011,3O(12):12O一124.
[12]朱权洁,姜福兴,尹永明等.基于小波分形特征与模式识别的矿山微震波形识别研究[J].岩土工程学报,2O12,34(11):2036—2042.
[13]吴贤振,焦永斌,陆哲祥.某铀矿井下中深孔爆破地表震动效应实测研[J].黄金,2005,26(10):15—18.
[14]PeitgenH O,JuergensH,SaupeD.混沌与分形 :科学的新疆界[M].2版.田逢春,译.北京 :国防工业出版社,2008:61—63.
[15]訾艳阳,胥永刚,何正嘉 .离散振动信号分形盒维数的改进算法和应用[J].机械科学与技术,2001,20(3):373—375